本题解相对于其他题解的特色有二:
一、深入分析了为什么要去重
二、给出了链式前项星的 线性去重方式
下面进入正文。
不难发现,将原图缩点成一个DAG后,图中的每一条链都是一个半连通子图,而最长的链就是最大半连通子图。
注意:新图中一个点的权值为这个点代表的SCC的点数,一个链的长度为各点权值之和。
统计最长链的权值不难,可以使用拓扑排序或记搜实现。为了避免引入STL影响效率,本文统一使用记搜。
本题的难点在统计方案数。
统计最小生成树方案数、最短路方案数等经典题的解法会给我们启示,紧紧抓住三角不等式这一核心算式,不断更新答案并继承方案数,这种方法依然使用本题。
但有所不同的是,本题需要考虑重边。
认真思考不难发现,传统的 tarjan 缩点得到的DAG中会出现重边(这里的重边是指从一个SCC指向另一个SCC的多条边)。
如果我们将前驱SCC的方案数累加给后继SCC,每一条连边都会发挥作用,导致答案过大。
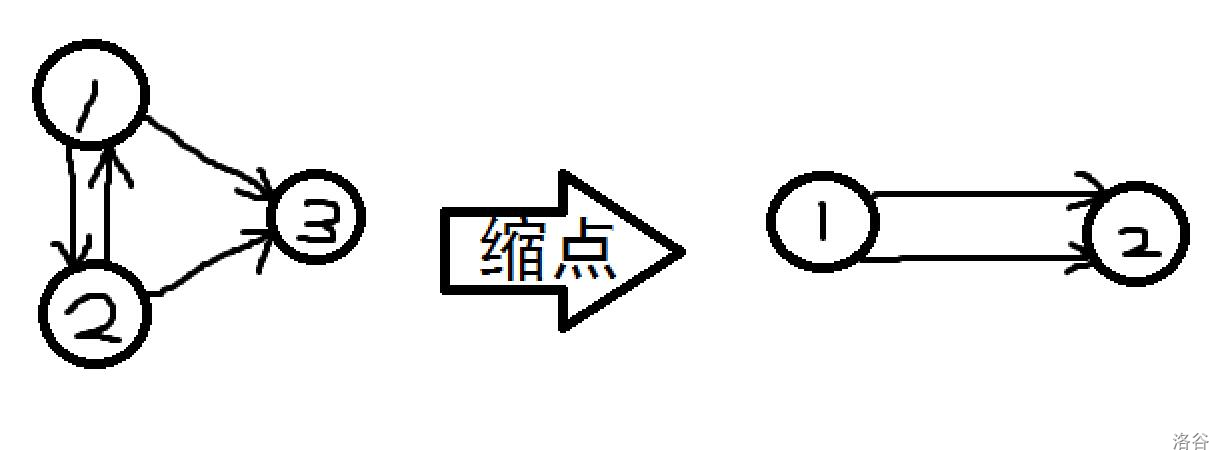
例如这张图:
手玩发现,最长链权值为 ,方案数为 。
然而,如果不去除重边,在右图中 号点更新答案时,同样意义的入边有两条,答案累加了两次,光荣WA掉。
因此,我们必须去重!
如何去重?我阅读了许多题解,发现主流方法有二
一是排序后标记重边,时间复杂度 ,且需要用到 STL ,可能需要用结构体存边并建立比较函数,时间常数和空间占用都很大;
二是排序后重新建图,时间复杂度 ,若使用 vector ,常数很大。
在此,我给出一种 的去除重边的方法
基于数组的链式前项星存图,把常数压榨到较小的水平
首先,链式前项星必备的三个数组和一个变量一定要有,他们分别是
int tot,head[MAXN],ver[MAXM],nxt[MAXM];
接下来,建立一个 ex[MAXN] 代表每个点是否被之前的某条边指过。
对于每一个点 ,遍历 的出边,标记出点,
若出现 ex[ver[nxt[i]]]==1 ,证明下一个被访问的出边所指向的点已经被 指过了,是重边。
重点:我们需要用到类似链表删除的操作,它是
nxt[i]=nxt[nxt[i]]
这代表着下一次访问 点时,原来的那个 会被跳过,直接访问到下一个的下一个。
注意:此处只用一个 if 删一次是不够的,需要用上 while 一直删到下一条边不是重边或者没有出边为止。
不难看出,原图中的每一条边至多被访问一遍就能完成删边操作,时间复杂度 。
由于超越了排序 的瓶颈,程序效率大幅提升。
总的时间复杂度是 。
下面贴上荣膺榜首的 代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define re register
#define MAXN 100010
#define MAXM 1000100
using namespace std;
int n,m,p,a,b;
int num,dfn[MAXN],low[MAXN];
int cnt,c[MAXN],dot[MAXN];
int top,stack[MAXN],ins[MAXN];
int ex[MAXN],tt[MAXN];
int ans,anss;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline int read() {
re int x = 0, f = 0;
re char ch = gc();
while(ch<'0'||ch>'9') f |= ch=='-', ch = gc();
while(ch>='0'&&ch<='9') {
x = (x<<3) + (x<<1) + (ch-'0');
ch = gc();
}
return f ? ~x+1 : x;
}
inline void write(int x) {
if(x<0) putchar('-'), x = ~x+1;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int tot,head[MAXN],ver[MAXM],nxt[MAXM];
inline void add(int x,int y) {
ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
}
inline void tarjan(int x) {
dfn[x] = low[x] = ++num;
stack[++top] = x, ins[x] = 1;
for(re int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if(!dfn[y]) {
tarjan(y);
low[x] = min(low[x],low[y]);
} else if(ins[y]) low[x] = min(low[x],dfn[y]);
}
if(dfn[x] == low[x]) {
int y;
++cnt;
do {
y = stack[top--], ins[y] = 0;
c[y] = cnt, ++dot[cnt];
} while(x != y);
}
}
int totw,hw[MAXN],vw[MAXM],nw[MAXM];
inline void addw(int x,int y) {
vw[++totw] = y, nw[totw] = hw[x], hw[x] = totw;
}
int v[MAXN],dis[MAXN],e[MAXN];
inline void dfs(int x) {
if(v[x]) return;
v[x] = 1, dis[x] = dot[x], e[x] = 1;
for(re int i = hw[x]; i; i = nw[i]) {
int y = vw[i];
dfs(y);
if(dis[y]+dot[x] > dis[x]) {
dis[x] = dis[y]+dot[x];
e[x] = 0;//这里先设0,后面会更新
//或者直接设e[x]=e[y],然后跳过循环
}
if(dis[y]+dot[x] == dis[x]) {
e[x] += e[y];
e[x] %= p;
}
}
}
int main() {
#ifdef hclove
freopen("a.in","r",stdin);
#endif
n = read(), m = read(), p = read();
for(re int i = 1; i <= m; ++i)
a = read(), b = read(), add(a,b);
for(re int i = 1; i <= n; ++i)
if(!dfn[i]) tarjan(i);
for(re int i = 1; i <= n; ++i)
for(re int j = head[i]; j; j = nxt[j])
if(c[i] != c[ver[j]]) addw(c[ver[j]],c[i]);
//这里是反向建新图,表示点都要用新图的点编号
for(re int i = 1; i <= cnt; ++i) {
// memset(ex,0,sizeof(ex));//死亡之memset,切忌!!!
for(re int j = hw[i]; j; j = nw[j]) {
ex[vw[j]] = 1;
while(j && ex[vw[nw[j]]])
nw[j] = nw[nw[j]];//线性去重的核心
}
for(re int j = hw[i]; j; j = nw[j])
ex[vw[j]] = 0;//要用这种方法清空
}
for(re int i = 1; i <= cnt; ++i)
if(!v[i]) dfs(i);
re int ans = 0;
re int anss = 0;
for(re int i = 1; i <= cnt; ++i)
ans = max(ans,dis[i]);
for(re int i = 1; i <= cnt; ++i)
if(dis[i] == ans) {
anss += e[i];
anss %= p;
}
write(ans), putchar('\n'), write(anss);
return 0;
}